Roulette parameters
Let us try to shed some light on roulette parameters and which numbers produce interesting shapes. Just by glancing at the grid of outcomes it is clear that teeth numbers wildly change the appearance of the curves. A fine control is only possible through a different set of parameters, namely what I call frequencies F=(T1/T,T3/T), or simply the teeth number ratios. This is continuation of the topics raised in the 1st article.
For TLDR: there is a short takeaway at the end of the article.
Ordinary spirograph is rather simple to predict. For instance both (105:63) and (140:84) will produce very similar curves since the ratio of the numbers is the same f0=n0/n1. We have f0=105/63=80/48=5/3. It is clear that any (5a:3a) spirograph will produce similar shape (a is arbitrary positive integer).
In a similar way, the 2nd order roulette (n0:n1;n2:n3) is governed with 2 ratios F=(f0,f1) where f0=n0/n1 and f1=n0⋅n2/(n1⋅n3). Somewhat of a complication is that the frequencies or ratios are best expressed as two fractions with smallest common denominator: F=(T1/T,T3/T). This is the same procedure as we would use to sum two fractions with different denominators. But the gain is that the numbers have immediate meaning: T is the number of times we turn inside the big static wheel n0, T3 is the number of lobes in the pattern, T1 is number of hoop turns, and their greatest common divisor nsymm=gcd(T1,T3) is the number of rotational symmetries.
1 Keep F=(T1/T,T3/T) the same
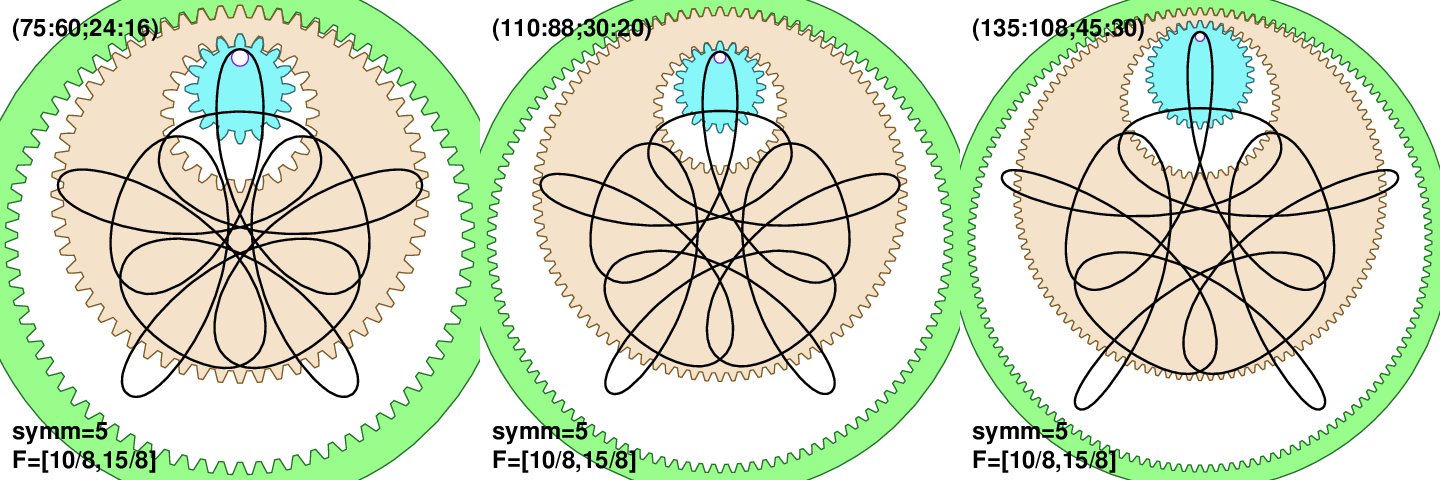
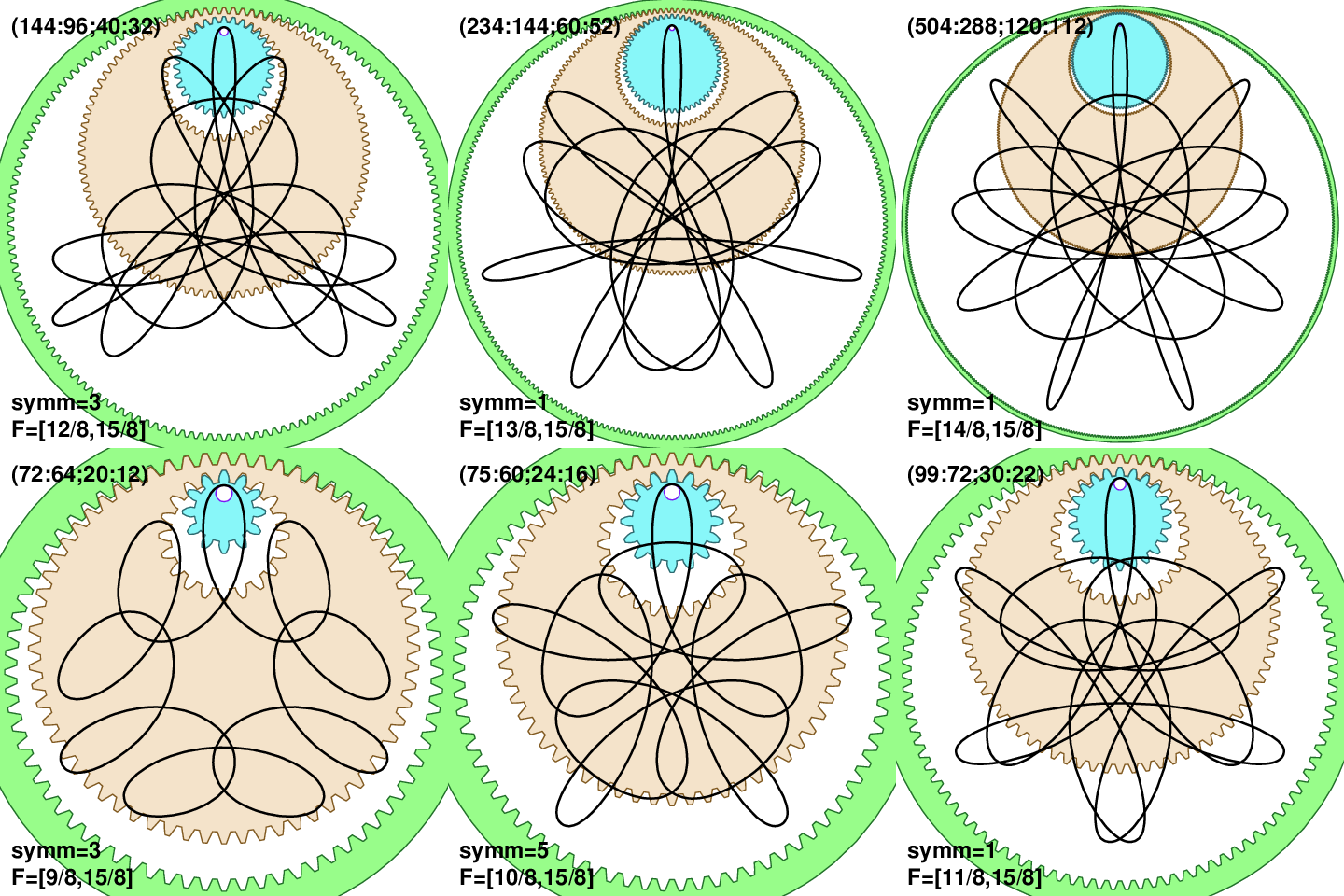
We can also calculate in the opposite direction: The two fractions F=(T1/T,T3/T) can be inverted to predict which teeth numbers (n0:n1;n2:n3) give the same curve. Lets use a simple example F=(10/8,15/8), which is a light 5-fold symmetric curve (5 is largest common factor of 10 and 15). Inversion gives us teeth numbers (5a:4a;3b:2b), which is ∞2 possibilities since a and b are arbitrary positive integers. I was still surprised to find that wild gears can accomplish that in 12 different ways: (75:60;24:16), (75:60;30:20), (100:80;54:36), (105:84;36:24), (110:88;30:20), (120:96;72:48), (135:108;45:30), (135:108;48:32), (135:108;63:42), (160:128;54:36), (160:128;96:64), and (200:160;81:54). The next figure shows 3 of those 12 different cog combinations (click on the image for larger version). While the curves are not exactly the same, as other parameters (such as hoop offset h or pen-hole distance p) influence amplitudes, it is clearly the very same type of pattern.
2 Change T for constant T1 and T3
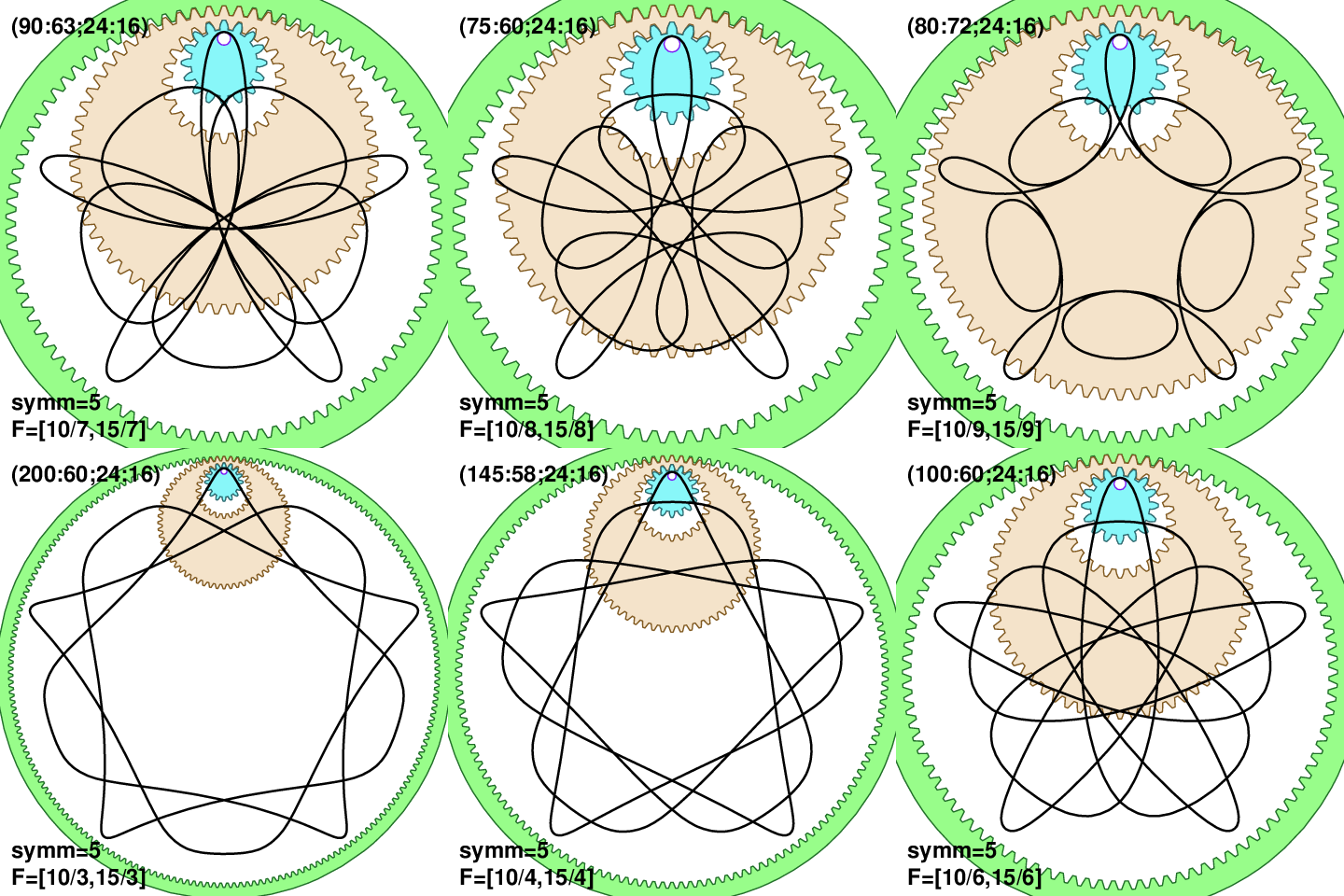
Next we can examine how does pattern change by keeping 2 out of 3 numbers T, T1, and T3 the same. So far I tried my best to keep everything reproducible with wild gears on paper. But from this point we are scanning through all possible combinations and not all choices are (yet?) possible with wild gears. The numbers T1 and T3 directly influence rotation symmetry nsymm=gcd(T1,T3), thus changing T and keeping T1 and T3 the same, is the smallest deviation from the nature of the pattern. The next figure shows T1=10 and T3=15, while T=3, 4, 6, 7, 8, and 9. Note that we have to keep T<T1<T3 (gears have to physically fit), and also T=5 is not available as it would divide both T1 and T3. The shown patterns have certain similarity.
A notable thing to observe is that the first panel F=(10/3,15/3) is the least interesting. Essentially that is because the gear elements are very different in size (the static wheel n0 is much bigger than the rest). This suggest that attractive curves probably require values T, T1 and T3 of somewhat similar order of magnitude, as that will produce similar size of cog elements.
3 Change T3 for constant T and T1
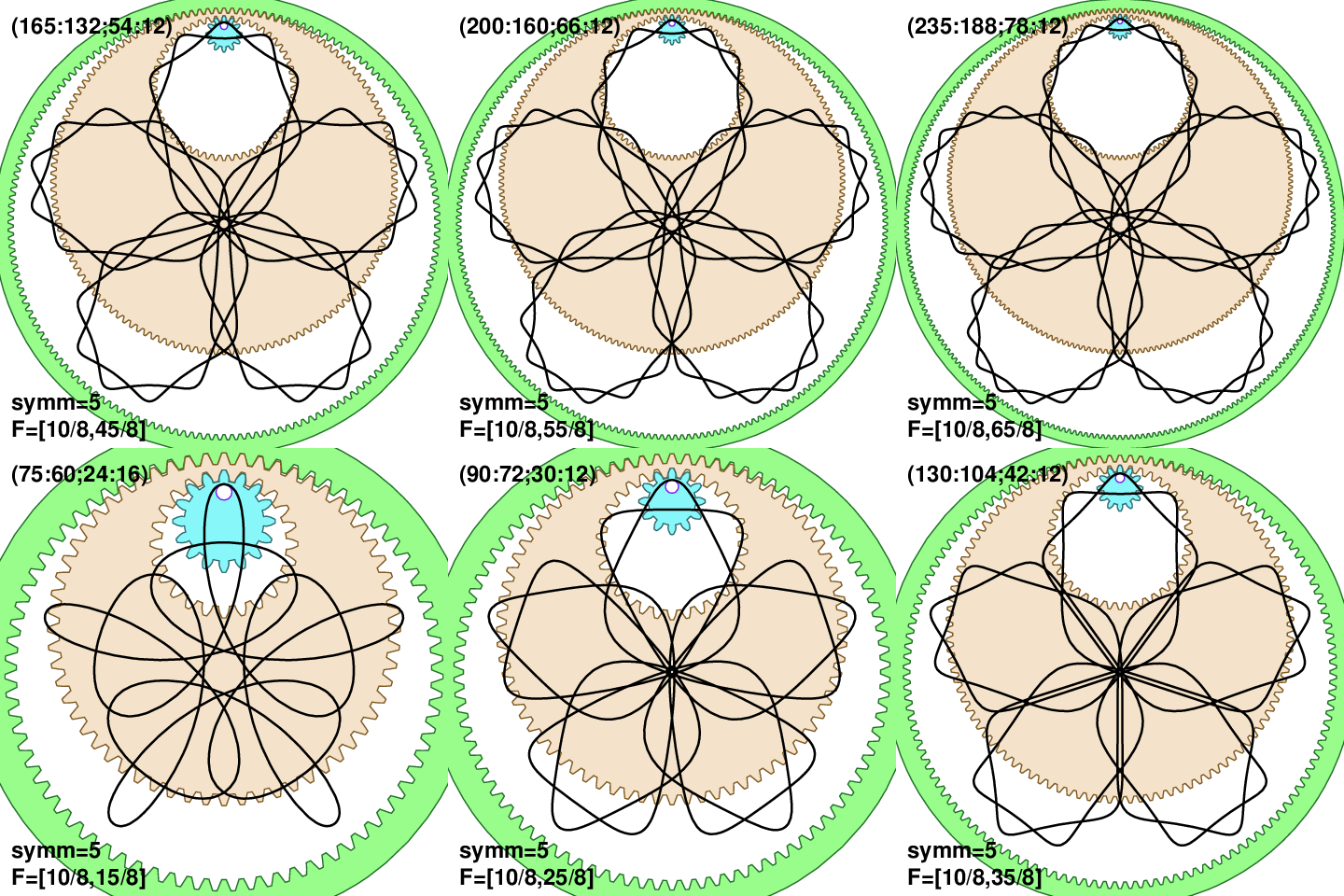
The next experiment is to change T3 while keeping T and T1 fixed. There are two versions, as we can decide to still keep rotation symmetry the same nsymm=5 (then T3=5+10k), or not (T3 is arbitrary: T3>T1). If we are to keep nsymm=5 then we have progression of T3 numbers: 15, 25, 35, 45, … Value T3=20 is not avaliable as it would give nsymm=10.
While there is similarity between panels (especially T3=15 and T3=25), the most apparent is how the gear n3 becomes smaller and smaller and the pattern looks more and more like a “ropy” ordinary spirograph. So again for the more interesting look T, T1 and T3 need similar order of magnitude.
We can also drop the requirement to keep nsymm=5. And then look at any value of T3>T1, but we need odd values of T3 since both T1 and T are already even:
This makes for an interesting figure. Symmetry is mostly lost, and that impacts the impression. However there is still a streak of similar details across the panels.
4 Change T1 for constant T and T3
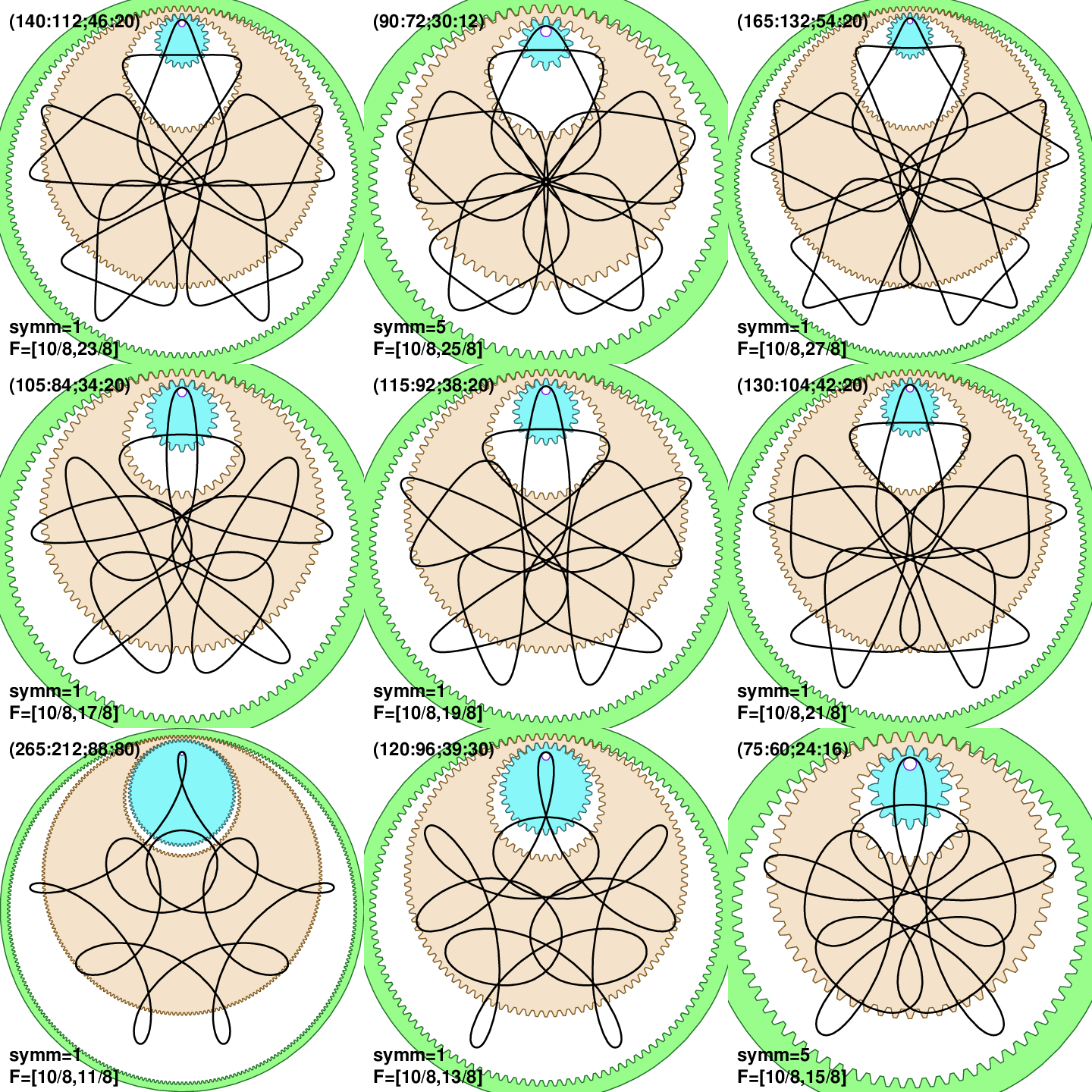
The last experiment is to keep T and T3 same, but change T1. Due to the choosen numbers and condition T<T1<T3 we can’t keep the same symmetry across panels:
Now there is less of similarity between panels. It is even hard to keep the same symmetry. This suggests that T1 is the most important in controlling the shape.
5 Summary
While one parameter study is not enough to be sure, our examples suggest three takeaway points:
-
Ratios F=(T1/T,T3/T) are the most important control of the curve shape.
-
Interesting patterns have 3 numbers T, T1, and T3, of similar magnitude.
-
T is least important, while T1 is the most important parameter.